大学物理の独言

物理学に関連して自分が学んだことを不定期で書いていきます。依頼や要望、ご指摘等はコメントまで

クラウジウス−クラペイロンの式

熱力学

ギブスエネルギー {G} はエネルギーによる効果とエントロピーによる効果をどちらも考慮して圧力一定下の変化の方向を調べるための指標で

\displaystyle G = H - TS

としてエンタルピー H と温度 T 、エントロピー S を用いて表現される。

このことから、ギブスエネルギーの変化量 dG が

\displaystyle dG = dH - T dS - S dT

と書かれることが言える。

エンタルピーの変化量は dH = pdV + Vdp + dU で、 dU = - pdV + dQ だから

\displaystyle dG = V dp + dQ - T dS - S dT

と書くことができる。

さらに、 dS = \dfrac{dQ}{T} なのだから、最終的に

dG = V dp - S dT

というように変形されて、ギブスエネルギーが圧力と温度の関数であることがわかる。

このことから、ギブスエネルギーを物質量で偏微分することによって表される化学ポテンシャル \mu = \dfrac{\partial G}{\partial n} も圧力と温度の関数であるといえる。

そんなわけで、化学ポテンシャルの微分形は

\displaystyle d \mu = \dfrac{\partial \mu}{\partial p} dp + \dfrac{\partial \mu}{\partial T}dT

と書けるのである。



H_2O の蒸気圧曲線について考えてみよう。

蒸気圧曲線上では液体の H_2O と気体の H_2O が平衡状態で存在しているわけだから、それぞれの化学ポテンシャルを \mu_l 、\mu_g とおけば

\displaystyle \mu_l = \mu_g

が成り立っている（これについては自由エネルギーについて書いたときに述べているので、そちらを参照してほしい）。

この関係から、当然 d\mu_l = d\mu_g が成り立つので、先ほど示した化学ポテンシャルの微分形を代入すると

\displaystyle \dfrac{\partial \mu_l}{\partial p}dp + \dfrac{\partial \mu_l}{\partial T}dT = \dfrac{\partial \mu_g}{\partial p}dp + \dfrac{\partial \mu_g}{\partial T}dT

という関係にあることがわかる。

これを変形すれば

\displaystyle dp = \dfrac{\dfrac{\partial \mu_g}{\partial T} - \dfrac{\partial \mu_l}{\partial T}}{\dfrac{\partial \mu_l}{\partial p} - \dfrac{\partial \mu_g}{\partial p}}dT

\displaystyle \dfrac{dp}{dT} = \dfrac{\dfrac{\partial \mu_g}{\partial T} - \dfrac{\partial \mu_l}{\partial T}}{\dfrac{\partial \mu_l}{\partial p} - \dfrac{\partial \mu_g}{\partial p}}

という変形ができるのである。

よくわからないので、もう少しの変形をしてみよう。

もともと化学ポテンシャルはギブスエネルギーを物質量で偏微分したものなのだから、純物質であれば

\mu = \dfrac{G}{n}

が成り立つ。

ギブスエネルギーの微分形からわかる通り、 \dfrac{\partial G}{\partial T} = - S 、 \dfrac{\partial G}{\partial p} = V が成り立つので

\displaystyle \dfrac{\partial \mu}{\partial T} = \dfrac{1}{n} \dfrac{\partial G}{\partial T} = - \dfrac{S}{n}

\displaystyle \dfrac{\partial \mu}{\partial p} = \dfrac{1}{n} \dfrac{\partial G}{\partial p} = \dfrac{V}{n}

という関係がわかる。

これをさきほどの \dfrac{dp}{dT} に代入すれば

\displaystyle \dfrac{dp}{dT} = \dfrac{S_l - S_g}{V_l - V_g}

がわかる。

H_2O の蒸発に伴うエントロピーの変化を \delta S 、体積の変化を \delta V とおけば

\displaystyle \dfrac{dp}{dT} = \dfrac{\delta S}{\delta V}

である。

周囲の圧力が大気圧で一定という普通の蒸発環境で考えれば \delta S = \dfrac{\delta H}{T} なので、これを代入すると

\displaystyle \dfrac{dp}{dT} = \dfrac{\delta H}{T \delta V}

とも書き換えられる。

この式はクラウジウス−クラペイロンの式と呼ばれる。

蒸気圧曲線はこれを満たすことになるので、横軸に温度、縦軸に圧力の蒸気圧グラフは、ある一つの温度での蒸気圧がわかれば直ちに描画できてしまうのである。

自由エネルギー

熱力学

下の図のような状況を考えてみてほしい。

容器の内部に気体が閉じ込められていることとし、内部のエントロピーは {S} 、外部はエントロピーが {S_{ex}} で温度が {T} とする。

容器の内側へ熱量 {dQ} が移動した場合、全体のエントロピー {S_{wh}} はどうなるだろうか。

f:id:monologue_physics:20210928155720p:plain

外部のエントロピーの微小変化 {dS_{ex}} は、微小な熱のやりとり程度では温度が変化しないと考えることができるので

{\displaystyle dS_{ex} = \dfrac{- dQ}{T}}

となる。

容器外部は {dQ} を失うので、上の表現では符号が負になっている。

容器内部のエントロピーの変化はそのまま {dS} としておけば、全体のエントロピーの変化は

{\displaystyle dS_{wh} = dS + dS_{ex}}

より

{\displaystyle dS_{wh} = dS - \dfrac{dQ}{T}}

として表すことができる。



定積変化になるようにピストンが固定されていた場合、移動する熱量が {dQ = dU} というふうに内部エネルギーを用いて表されるので、全体のエントロピーは

{\displaystyle dS_{wh} = dS - \dfrac{dU}{T}}

というように書き換えられる。

この右辺は {d\left( S - \dfrac{U}{T} \right)} と書き換えることができ、( ) の内部に {T} をかけて符号を逆転させたものを {A} と書くことにすると、

{\displaystyle A = U - TS}

となり、この {A} をヘルムホルツエネルギーという。

定圧変化の場合も同様に考えてみると、定圧変化では {dQ = dH} というようにエンタルピーを用いて移動する熱量を表せるから

{\displaystyle dS_{wh} = dS - \dfrac{dH}{T}}

で、{A} ではなく {G} を用いれば

{\displaystyle G = H - TS}

と書くことができる。

この {G} はギブスエネルギーと呼ばれる。

ヘルムホルツエネルギーとかギブスエネルギーをまとめて自由エネルギーと呼ぶが、これを導入すると、エネルギーとエントロピー両方の影響を考慮した系の変化の様子を調べることができる。

これらの導入は、化学変化の方向を考えるのに非常に有用である。

エントロピーは一定に保たれるか増加するかのどちらかしか起こらないので、{dS_{wh} \geq 0} とならなければならない。

そのため、系の変化は、定積変化では {dA \leq 0} を満たすものしか起こらず、定圧変化の場合にも {dG \leq 0} を満たす。

エントロピーは放置していれば平衡状態（{dS_{wh} = 0}）になるまで増大するので、定積変化の場合には {dA \lt 0}、定圧変化の場合には {dG \lt 0} の状態では変化が自発的に進行し、{dA = 0, \: dG = 0} のところで平衡を迎えて変化が停止することになる。



ひとつ例を考えてみよう。

f:id:monologue_physics:20210928164954p:plain

密閉容器（圧力一定）が気体の水 {n_1 [mol]} が存在する系（系1）と液体の水 {n_2 [mol]} が存在する系（系2）に分かれているとする。

定圧変化なのでギブスエネルギーを用いて考えることができ、系1と系2のギブスエネルギーをそれぞれ {G_1} 、{G_2} とおけば、系全体のギブスエネルギーは {G = G_1 + G_2} と書くことができる。

ギブスエネルギーは物質量に依存するので {dG_1 = \dfrac{\partial G_1}{\partial n_1} dn_1}、 {dG_2 = \dfrac{\partial G_2}{\partial n_2} dn_2} と表せるから

{\displaystyle dG = \dfrac{\partial G_1}{\partial n_1} dn_1 + \dfrac{\partial G_2}{\partial n_2} dn_2}

となる。

これが 0 になるところで気液平衡に達することになる。

系2から減少した物質量だけ系1の物質量が増加するので {dn_2 = -dn_1} が成り立ち、これを代入すれば

{\displaystyle dG = \left( \dfrac{\partial G_1}{\partial n_1} - \dfrac{\partial G_2}{\partial n_2} \right) dn_1}

が得られる。

化学ポテンシャル {\mu_1 = \dfrac{\partial G_1}{\partial n_1}}と {\mu_2 = \dfrac{\partial G_2}{\partial n_2}} を定義すると、

{\displaystyle \mu_1 = \mu_2}

となるところで気液平衡を迎えるのである。

エントロピー・熱力学第二法則

熱力学

カルノーサイクルを例に考えた熱機関で得られた式からエントロピー {S = \dfrac{Q}{T}} を定義した。

今回は、エントロピーについてもう少し詳しくみていきたい。

まず、系全体のエントロピー {S_{sum}} というのは、系を {n} 個の区間に区切ってその {i} 番目の位置のエントロピーを {S_i} とおけば

{\displaystyle S_{sum} = \sum_i S_i}

として表すことができる。

つまり、系全体のエントロピーは、系を構成するひとつひとつの場所のエントロピーの和で与えられる。

極端なことを言えば、{S_{sum}} は宇宙全体で定義するべきだろう。

エントロピーが増大するだとか可逆変化では一定だとかというのは宇宙全体で考えたときの {S_{sum}} の話で、ひとつひとつの部分についての話ではない。

ある部分のみを見たらエントロピーが減少するような変化でも、宇宙全体で考えれば {S_{sum}} は一定になるか増加しているはずだ。

しかし、そこまで極端に視野を広げなくとも、変化が起きない部分はそもそもエントロピーが一定となっているから見る場所を制限しても問題ないという理屈である。



次に、エントロピーの変化量について見ておこう。

熱力学第一法則から導出されたように、受け取る熱量 {Q} というのは、エンタルピーを {H} 、内部エネルギーを {U} とおけば定圧変化では {Q = \Delta H} 、定積変化では {Q = \Delta U} として表される。

エントロピーの定義からその変化量が

{\displaystyle dS = \dfrac{dQ}{T}}

と表されることを考えると、定圧変化でのエントロピー変化は

{\displaystyle dS = \dfrac{dH}{T}}

である。

エンタルピーが {H = n C_p T} と表されることから {dH = n C_p dT} で、定圧変化におけるエントロピーは

{\displaystyle S = \int_{T_0}^{T_1} \dfrac{n C_p}{T} dT}

として計算されることになる。

モル熱容量というのは一般には温度によって変化するので、積分の外に出すことはできない。

定積変化の場合についても、考え方はあまり変わらない。

定積変化で {Q = \Delta U} なのだから、エンタルピーの変化は

{\displaystyle dS = \dfrac{dU}{T}}

となる。

{U = n C_v T} より {dU = n C_v dT} で、

{\displaystyle S = \int_{T_0}^{T_1} \dfrac{n C_v}{T} dT}

によって計算することができる。



最後に、熱力学第二法則を紹介しておこう。

この法則の主張は、「熱は温度の高いものから低いものへ移動し、逆方向の移動は起こらない」という直感通りのもので、エントロピーから説明ができる。

下の図のような例で考えてみよう。

周囲を断熱材で覆われた容器が温度の異なるふたつの部屋（ROOM 1, ROOM 2）に区切られ、ROOM 1 から ROOM 2 にむけて {dQ} の熱が移動するとする。

つまり、実際には {dQ} が正であればROOM 1 から ROOM 2 へ熱が移動するし、負であれば ROOM 2 から ROOM 1 へ移動するわけである。

考えている熱量が微小なので、{dQ} の移動程度では両部屋の温度は変わらないと見てよい。

f:id:monologue_physics:20210927135435p:plain

このとき、熱の移動が起こるのは両部屋間だけで外には一切影響しないので、エントロピーの変化を考えなければならないのは断熱材に覆われた内部だけということになる。

ROOM 1 の熱量の変化は {- dQ} だから、この部屋のエントロピーの変化は

{\displaystyle dS_1 = \dfrac{-dQ}{T_1}}

で、同様に ROOM 2 の熱量の変化は {+ dQ} だから

{\displaystyle dS_2 = \dfrac{dQ}{T_2}}

となる。

これらから、系全体のエントロピーの変化は

{\displaystyle \begin{split} dS &= dS_1 + dS_2 \\ \\ \displaystyle &= \left( - \dfrac{1}{T_1} + \dfrac{1}{T_2} \right) dQ \\ \\ \displaystyle &= \dfrac{T_1 - T_2}{T_1 T_2} dQ \end{split}}

というように求まる。

エントロピーは減少しないのだから {dS \gt 0} により

{\displaystyle \left\{ \begin{array}{lr} dQ \gt 0 & \left( if \; T_1 \gt T_2 \right) \\ \\ \displaystyle dQ \lt 0 & \left( if \; T_1 \lt T_2 \right) \end{array} \right.}

とならなければならず、熱力学第二法則が証明される。

カルノーサイクル・エントロピー

熱力学

熱機関と熱力学の発展は切っても切り離せない関係にあるので、カルノーサイクルというものについてここで扱っておきたい。

カルノーサイクルというのは、下の図のように断熱変化と等温変化の繰り返しによってピストンを動かす熱機関である。

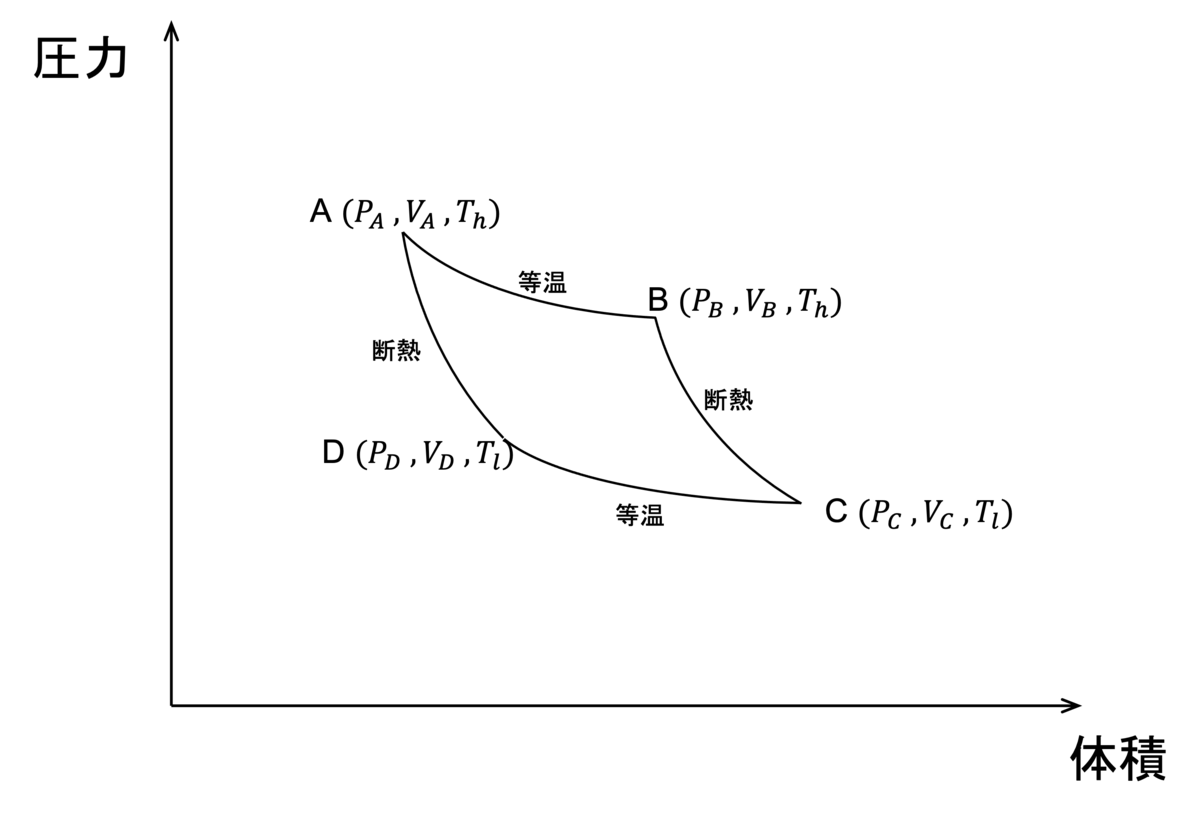
f:id:monologue_physics:20210926141048p:plain

サイクルの向きはA→B→C→D→A→... とし、図に示したように過程A→BとC→Dは等温変化、B→CとD→Aは断熱変化で、閉じ込められた気体の体積と圧力を変化させる。

また、ふたつの等温変化の過程では外部と熱のやり通りをすることとし、A→Bでは {Q_h} の熱量が供給され、C→Dでは {Q_l} の熱量が排出されるようにする。

以上の条件で、カルノーサイクルの熱効率（受け取ったエネルギーに対してどれだけの仕事をできるか）を考えていこう。



まず、A→Bにおいて、外部に対してする仕事 {w_{AB}} は、気体の状態方程式を用いれば

{\displaystyle w_{AB} = \int_{V_A}^{V_B} p dV = \int_{V_A}^{V_B} \dfrac{nRT_h}{V} dV}

であるから

{\displaystyle w_{AB} = nRT_h \log{\dfrac{V_B}{V_A}}}

となる。

次にB→Cだが、ここでは断熱過程であるから、熱力学第一法則より外部にした仕事は気体の内部エネルギーの変化量と等しくなる。

このことから

{\displaystyle w_{BC} = n C_v \left( T_l - T_h \right)}

である。

同じように考えれば、C→Dは等温変化だから

{\displaystyle w_{CD} = nRT_l \log{\dfrac{V_D}{V_C}}}

D→Aは断熱変化だから

{\displaystyle w_{DA} = n C_v \left( T_h - T_l \right)}

となる。

熱効率 {\eta} というのは受け取ったエネルギーに対して外部にすることのできる仕事はどれくらいかというのを表すから、その定義から

{\displaystyle \eta = \dfrac{w_{AB} + w_{BC} + w_{CD} + w_{DA}}{Q_h}}

である。

A→Bは等温過程であることから熱力学第一法則により

{\displaystyle Q_h = w_{AB}}

となることを考慮すると、上での計算結果を代入すれば

{\displaystyle \eta = \dfrac{nRT_h \log{\dfrac{V_B}{V_A}} + nRT_l \log{\dfrac{V_D}{V_C}}}{nRT_h \log{\dfrac{V_B}{V_A}}}}

ということになる。

ここで、B→CとD→Aというふたつの断熱変化について考えると、

{\displaystyle T_h V_B^{\frac{C_p}{C_v} - 1} = T_l V_C^{\frac{C_p}{C_v} - 1}}

{\displaystyle T_h V_A^{\frac{C_p}{C_v} - 1} = T_l V_D^{\frac{C_p}{C_v} - 1}}

となるから、これにより

{\displaystyle \begin{split} \left( \dfrac{V_A}{V_B} \right)^{\frac{C_p}{C_v} - 1} &= \left( \dfrac{V_D}{V_C} \right)^{\frac{C_p}{C_v} - 1} \\ \\ \displaystyle \dfrac{V_A}{V_B} &= \dfrac{V_D}{V_C} \end{split}}

という関係になっていることがわかる。

さきほどの {\eta} に代入すれば

{\displaystyle \eta = \dfrac{T_h - T_l}{T_h} = 1 - \dfrac{T_l}{T_h}}

というシンプルな形として、熱効率が求まるのである。

さらに、外部へする仕事 {w_{sum}} をエネルギー保存則から考えれば {w_{sum} = Q_h - Q_l} となるのだから、熱効率は

{\displaystyle \eta = \dfrac{Q_h - Q_l}{Q_h} = 1 - \dfrac{Q_l}{Q_h}}

とも書くことができる。

熱効率を温度を用いて表した場合と比べてみると

{\displaystyle 1 - \dfrac{T_l}{T_h} = 1 - \dfrac{Q_l}{Q_h}}

により

{\displaystyle \dfrac{Q_h}{T_h} = \dfrac{Q_l}{T_l}}

がわかる。

この {S = \dfrac{Q}{T}} をエントロピーと呼ぶ。

エントロピーは系の乱雑さを表しており、可逆な変化はエントロピーが一定となることが知られている。

実際、カルノーサイクルでは先ほど考えたのと逆方向の D→C→B→A→D→... というような変化を自発的に起こすことができるのだからこれは可逆変化で、エントロピーが一定となることは熱効率についての議論からたしかめた。

不可逆な変化ではエントロピーが大きくなり、エントロピーが小さくなる変化は起こらない。

エントロピーというのは場合の数から考えることができるのだが、例えば 0 か 1 をランダムで表示するモニターが n 個あったとき、全てが 0 、または全てが 1 を表示する確率は、n 個のうち半分が 0 、もう半分が 1 を表示する確率に比べて低く、全てが同じ数字を表示する可能性は n が大きくなればほとんどなくなってしまう。

エントロピーを考えるときの乱雑さというのは上の例で言えば 0 と 1 が入り混じっている状態ということになり、表示する数字を変化させていった場合、入り混じった状態から一方の数字に偏っていく（エントロピーが小さくなる）ことは確率論的にありえないと言ってよいが、偏った状態から入り混じった状態に変化していく（エントロピーが大きくなる）ことは当たり前に起こるのである。

エントロピーについては、別の記事でもう少し詳しく書いている。

断熱変化

熱力学

気体が受け取る熱量は、閉じ込められた気体の体積が一定となる場合は気体の内部エネルギーの変化と等しくなるし、圧力が一定となる場合はエンタルピーの変化と等しくなる。

では、受け取る熱量を 0 にしてしまった場合には気体はどう変化するのだろうか。

この変化は外部との熱のやりとりを断つ変化ということで断熱変化と呼ばれるが、この場合の熱力学第一法則は {q = 0} となるのだから

{\displaystyle \Delta U + w = 0}

と書くことができる。

気体の定積モル熱容量 {C_v} は

{\displaystyle C_v = \dfrac{1}{n} \left( \dfrac{\partial U}{\partial T} \right)_v}

と書かれるのだから、{dU = n C_v dT} である。

また、仕事 {w} が {w = p dV} であることから、気体の状態方程式を用いれば微小仕事は

{\displaystyle p dV = \dfrac{nRT}{V} dV}

となる。

以上のことを熱力学第一法則に適用してみると、微小な変化について

{\displaystyle n C_v dT + \dfrac{nRT}{V} dV = 0}

と書けるようになる。

これを変数分離の後に積分してみれば、

{\displaystyle \begin{split} \int_{T_0}^{T_1} \dfrac{n C_v}{T} dT + \int_{V_0}^{V_1} \dfrac{nR}{V} dV &= 0 \\ \\ \displaystyle C_v \log{T_1} + R \log{V_1} &= C_v \log{T_0} + R \log{V_0} \\ \\ \displaystyle \log{T_1 V_1^\frac{R}{C_v}} &= \log{T_0 V_0^\frac{R}{C_v}} \\ \\ \displaystyle T_1 V_1^\frac{R}{C_v} &= T_0 V_0^\frac{R}{C_v} \end{split}}

マイヤーの関係式により {R = C_p - C_v} となることを用いれば

{\displaystyle T_1 V_1^{\frac{C_p}{C_v} - 1} = T_0 V_0^{\frac{C_p}{C_v} - 1}}

{T_0, V_0} と {T_1. V_1} の関係は特に定めていないので、任意の変化について

{\displaystyle T V^{\frac{C_p}{C_v} - 1} = Constant}

が成り立つことになる。

気体の状態方程式 {T = \dfrac{pV}{nR}} を代入すると、物質量も気体定数も一定であることを考慮して

{\displaystyle p V^\frac{C_p}{C_v} = Constant}

と書き換えることもできる。

断熱変化では、気体の物質量が一定である限りこの関係が成立するのである。

熱容量・マイヤーの関係式

熱力学

熱力学第一法則から、熱容量について考えてみる。

熱容量 {C} というのは、ある熱量を受け取ったときに温度がどの程度変化するかというのを表す比例係数で、その定義は

{\displaystyle C = \dfrac{dq}{dT}}

となる。

ここで、{q} は受け取った熱量、{T} は温度を表す。

つまり、{q} の微分の形で表せば

{\displaystyle dq = C dT}

と表され、両辺を積分すれば

{\displaystyle q = \int_{T_0}^{T} C dT}

である。

{C} は物質の構造によって異なる値を持つが、それだけでなく、温度によっても変化する。

そのため、一般には積分の外に出すことはできない。

今回は、いくつかの条件下での熱容量がどのように表されるかというのを考えてみたい。



熱力学第一法則は、気体が受け取る熱量を {q} 、外に対してする仕事を {w} 、気体の内部エネルギーの変化を {\Delta U} とおけば

{\displaystyle q = w + \Delta U}

と書けるのだった。

まず、定積過程について考えてみよう。

定積過程というのは体積が変化しないのだから、もちろん {w = 0} である。

よって、熱力学第一法則は

{\displaystyle q = \Delta U}

となり、定積過程での熱容量 {C_v} は

{\displaystyle C_v = \left( \dfrac{dq}{dT} \right)_v = \left( \dfrac{dU}{dT} \right)_v}

と書けるようになる。

右辺の {\left( \: \right)_v} というのは、体積が一定という状況について考えていることを明示している。

気体の内部エネルギーは気体の物質量 {n} に比例するわけだから定積過程の熱容量も物質量に比例するようになるわけだが、この要素を取り除いた1モルあたりの定積熱容量 {C_{v, m}}を考えれば

{\displaystyle C_{v, m} = \dfrac{1}{n} \left( \dfrac{dU}{dT} \right)_v}

ということになり、1モルあたりの定積熱容量は定積モル熱容量と呼ばれる。



次に、定圧過程について考える。

定圧過程で受け取る熱量は、エンタルピー {H} に等しい。

この性質を使って考えると、定圧熱容量 {C_p} は

{\displaystyle C_p = \left( \dfrac{dq}{dT} \right)_p = \left( \dfrac{dH}{dT} \right)_p}

と書けることがわかる。

定積過程について行った時と同様に、{\left( \: \right)_p} は圧力一定という状況を表すためのものである。

また、定圧モル熱容量 {C_{p, m}} を考えれば

{\displaystyle C_{p, m} = \dfrac{1}{n} \left( \dfrac{dH}{dT} \right)_p}

となる。



定圧モル熱容量について、もう少し別の表現を考えてみたい。

{w} は圧力 {p} と気体の体積 {V} を用いて

{\displaystyle w = p \Delta V}

と表されるが、気体定数を {R} とおけば気体の状態方程式により

{\displaystyle pV = nRT}

と書けるから、物質量を一定とすると

{\displaystyle p \Delta V = nR \Delta T}

である。

これを使って定圧モル熱容量 {C_{p, m}} を考えると

{\displaystyle C_{p, m} = \dfrac{1}{n} \left( \dfrac{dq}{dT} \right)_p = R + \dfrac{1}{n} \left( \dfrac{dU}{dT} \right)_p}

と表せるようになる。

気体の内部エネルギー {U} というのは、気体分子運動論から考えればわかるように、物質量一定の条件では温度のみの関数であるから、圧力を一定にして体積を変化させた場合と体積を一定にして圧力を変化させた場合では、温度の変化幅に対する内部エネルギーの変化量は全く同じである。

つまり、圧力と体積でどちらを変化させるかというのに関係なく、気体の内部エネルギーの変化量は温度の変化量のみによって決定される。

このことから

{\displaystyle \left( \dfrac{dU}{dT} \right)_p = \left( \dfrac{dU}{dT} \right)_v}

がわかる。

これをさきほどの定圧モル熱容量の表現に代入してみると

{\displaystyle C_{p, m} = R + \dfrac{1}{n} \left( \dfrac{dU}{dT} \right)_v}

と書き換えることができ、右辺第二項に定積モル熱容量を代入してやれば

{\displaystyle C_{p, m} = R + C_{v, m}}

が成り立つ。

もちろん、両辺に物質量をかければ

{\displaystyle C_p = R + C_v}

となる。

このような定積（モル）熱容量と定圧（モル）熱容量の関係式をマイヤーの関係式と呼ぶ。

熱力学第一法則・エンタルピー

熱力学

私が熱力学第一法則を高校で学んだとき、それを覚えるものとして指導された。

その後いくつかの本を読んでも同じように暗記しなければならないかのように扱われていて、何人かの友人は「される仕事の場合は符号が...」などと苦労していたのだが、実際にはもっとシンプルなものである。

この法則は、ようはエネルギー保存則だ。

気体が受け取った熱を {q} 、内部エネルギーの変化量を {\Delta U} 、気体がされた仕事を {w} とおけば、熱力学第一法則は

{\displaystyle \Delta U = q + w}

となる。

これは気体が受け取った熱とされた仕事がそのまま内部エネルギーに変化しているということを表しているのだから、ただ単に「受け取ったエネルギーの分だけ内部エネルギーが増加する」というだけの意味となる。

だから、気体が外に向けてした仕事を {w} とおくことにするなら

{\Delta U = q - w}

というふうになるのも、覚えていなくたって少し考えればわかる。



そうは言っても、いちいち仕事が「される」なのか「する」なのかを考えながら式を作るのはめんどくさい。

する仕事 {w} の定義は、働く力を {F} 、力と垂直な方向への変位を {\delta x} とおけば

{\displaystyle w = \int_{x_0}^{x_0 + \delta x} F dr}

である。

{F} を圧力 {p} を用いて表してみると、力を受ける面積を {S} とすれば

{\displaystyle F = pS}

となるのだから、体積 {V} を用いて

{\displaystyle w = \int_{x_0}^{x_0 + \delta x} pS dr = \int_{V_0}^{V_0 + \delta V} p dV}

と書けるようになる。

この書き換えを用いれば、する仕事は {\Delta V} が正だし、される仕事は {\Delta V} が負なので、一律に

{\displaystyle w = - \int_{V_0}^{V_0 + \delta V} p dV}

と書くことができるようになる。

ここからわかるように、圧力が一定な変化（定圧過程）では

{\displaystyle w = p \Delta V}

だし、体積が一定な変化（定積過程）では

{\displaystyle w = 0}

となる。



ここで、エンタルピーという新しい関数を導入しておこう。

エンタルピー {H} は

{\displaystyle H = U + pV}

で定義される。

すると、エンタルピーの変化量は

{\displaystyle \Delta H = \Delta U + p \Delta V + V \Delta p}

と表されるようになる。

圧力が一定という条件について考えると、右辺の最後の項が消えるから、エンタルピーの変化は圧力一定下での熱力学第一法則における気体が受け取った熱量 {q} と等しくなる。

化学変化を扱うときなどでは圧力一定で変化を起こすことが多い（外気に晒したまま反応を起こさせるため、圧力は外気圧で一定となる）から、エンタルピーは非常に活躍する。

では、ここで除け者にされてしまった右辺第三項の {V \Delta p} は何かというと、外に向けて仕事をするために気体が蓄えている能力というような意味合いに解釈ができる。

体積一定条件では

{\displaystyle \Delta H = \Delta U + V \Delta p}

となるのだから、エンタルピーの変化量が内部エネルギーの変化量と仕事をする能力の蓄えということになる。