大学物理の独言

物理学に関連して自分が学んだことを不定期で書いていきます。依頼や要望、ご指摘等はコメントまで

カルノーサイクル・エントロピー

熱力学

熱機関と熱力学の発展は切っても切り離せない関係にあるので、カルノーサイクルというものについてここで扱っておきたい。

カルノーサイクルというのは、下の図のように断熱変化と等温変化の繰り返しによってピストンを動かす熱機関である。

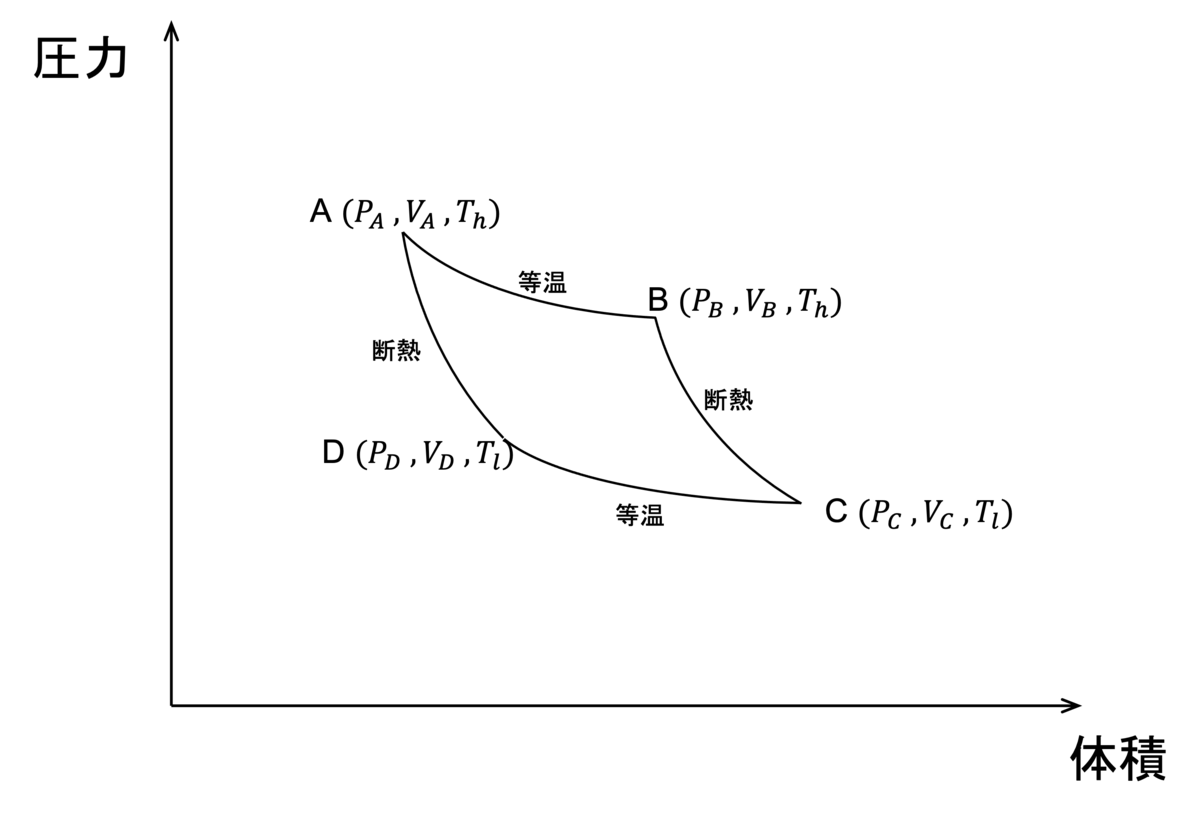
f:id:monologue_physics:20210926141048p:plain

サイクルの向きはA→B→C→D→A→... とし、図に示したように過程A→BとC→Dは等温変化、B→CとD→Aは断熱変化で、閉じ込められた気体の体積と圧力を変化させる。

また、ふたつの等温変化の過程では外部と熱のやり通りをすることとし、A→Bでは {Q_h} の熱量が供給され、C→Dでは {Q_l} の熱量が排出されるようにする。

以上の条件で、カルノーサイクルの熱効率（受け取ったエネルギーに対してどれだけの仕事をできるか）を考えていこう。



まず、A→Bにおいて、外部に対してする仕事 {w_{AB}} は、気体の状態方程式を用いれば

{\displaystyle w_{AB} = \int_{V_A}^{V_B} p dV = \int_{V_A}^{V_B} \dfrac{nRT_h}{V} dV}

であるから

{\displaystyle w_{AB} = nRT_h \log{\dfrac{V_B}{V_A}}}

となる。

次にB→Cだが、ここでは断熱過程であるから、熱力学第一法則より外部にした仕事は気体の内部エネルギーの変化量と等しくなる。

このことから

{\displaystyle w_{BC} = n C_v \left( T_l - T_h \right)}

である。

同じように考えれば、C→Dは等温変化だから

{\displaystyle w_{CD} = nRT_l \log{\dfrac{V_D}{V_C}}}

D→Aは断熱変化だから

{\displaystyle w_{DA} = n C_v \left( T_h - T_l \right)}

となる。

熱効率 {\eta} というのは受け取ったエネルギーに対して外部にすることのできる仕事はどれくらいかというのを表すから、その定義から

{\displaystyle \eta = \dfrac{w_{AB} + w_{BC} + w_{CD} + w_{DA}}{Q_h}}

である。

A→Bは等温過程であることから熱力学第一法則により

{\displaystyle Q_h = w_{AB}}

となることを考慮すると、上での計算結果を代入すれば

{\displaystyle \eta = \dfrac{nRT_h \log{\dfrac{V_B}{V_A}} + nRT_l \log{\dfrac{V_D}{V_C}}}{nRT_h \log{\dfrac{V_B}{V_A}}}}

ということになる。

ここで、B→CとD→Aというふたつの断熱変化について考えると、

{\displaystyle T_h V_B^{\frac{C_p}{C_v} - 1} = T_l V_C^{\frac{C_p}{C_v} - 1}}

{\displaystyle T_h V_A^{\frac{C_p}{C_v} - 1} = T_l V_D^{\frac{C_p}{C_v} - 1}}

となるから、これにより

{\displaystyle \begin{split} \left( \dfrac{V_A}{V_B} \right)^{\frac{C_p}{C_v} - 1} &= \left( \dfrac{V_D}{V_C} \right)^{\frac{C_p}{C_v} - 1} \\ \\ \displaystyle \dfrac{V_A}{V_B} &= \dfrac{V_D}{V_C} \end{split}}

という関係になっていることがわかる。

さきほどの {\eta} に代入すれば

{\displaystyle \eta = \dfrac{T_h - T_l}{T_h} = 1 - \dfrac{T_l}{T_h}}

というシンプルな形として、熱効率が求まるのである。

さらに、外部へする仕事 {w_{sum}} をエネルギー保存則から考えれば {w_{sum} = Q_h - Q_l} となるのだから、熱効率は

{\displaystyle \eta = \dfrac{Q_h - Q_l}{Q_h} = 1 - \dfrac{Q_l}{Q_h}}

とも書くことができる。

熱効率を温度を用いて表した場合と比べてみると

{\displaystyle 1 - \dfrac{T_l}{T_h} = 1 - \dfrac{Q_l}{Q_h}}

により

{\displaystyle \dfrac{Q_h}{T_h} = \dfrac{Q_l}{T_l}}

がわかる。

この {S = \dfrac{Q}{T}} をエントロピーと呼ぶ。

エントロピーは系の乱雑さを表しており、可逆な変化はエントロピーが一定となることが知られている。

実際、カルノーサイクルでは先ほど考えたのと逆方向の D→C→B→A→D→... というような変化を自発的に起こすことができるのだからこれは可逆変化で、エントロピーが一定となることは熱効率についての議論からたしかめた。

不可逆な変化ではエントロピーが大きくなり、エントロピーが小さくなる変化は起こらない。

エントロピーというのは場合の数から考えることができるのだが、例えば 0 か 1 をランダムで表示するモニターが n 個あったとき、全てが 0 、または全てが 1 を表示する確率は、n 個のうち半分が 0 、もう半分が 1 を表示する確率に比べて低く、全てが同じ数字を表示する可能性は n が大きくなればほとんどなくなってしまう。

エントロピーを考えるときの乱雑さというのは上の例で言えば 0 と 1 が入り混じっている状態ということになり、表示する数字を変化させていった場合、入り混じった状態から一方の数字に偏っていく（エントロピーが小さくなる）ことは確率論的にありえないと言ってよいが、偏った状態から入り混じった状態に変化していく（エントロピーが大きくなる）ことは当たり前に起こるのである。

エントロピーについては、別の記事でもう少し詳しく書いている。