慣性モーメントと回転の運動方程式

質点の運動について考えるのは力学では最も初歩的で基礎となるが、実際のところ質点として考えることのできる物体は多くなく、大抵の場合はその回転運動などの要素も考慮しなければならない。

そこで、剛体という概念を導入し、もう少し日常で起こる現象に近づいた考察を試みるのである。

剛体とは、大きさや形が決して変化することのない固体のことを言う。

つまり、剛体について考える時には、その物体を構成する原子同士の距離が決して変化することなく一定であるとする。

つまり、実際には物体のある部分が受けた力は原子同士の距離の関係が変化することによって全体に伝わるわけであるが、剛体として考える場合には、ある部分に力が加わるとそれが瞬時に物体全体に伝わると考えるのである。

残念ながらこのような考え方も近似に他ならず、実際には剛体などと言うものは存在しない。

なぜならば、相対性理論によれば、物質やエネルギーが光速を超えた速さで伝わることは起こり得ず、瞬時に伝わるとする仮定はこれと矛盾するためである。

しかし、そうは言ってもこの近似は非常に便利で、簡単な運動を考察するには充分である。

さて、質点では考える必要がなくて剛体では考えなければならない重要な要素である回転について考察していこう。

剛体は無数の質点から成ると考えることができるため、下の図のように回転の中心を原点とする座標系でそのひとつひとつについて考えていくことにする。

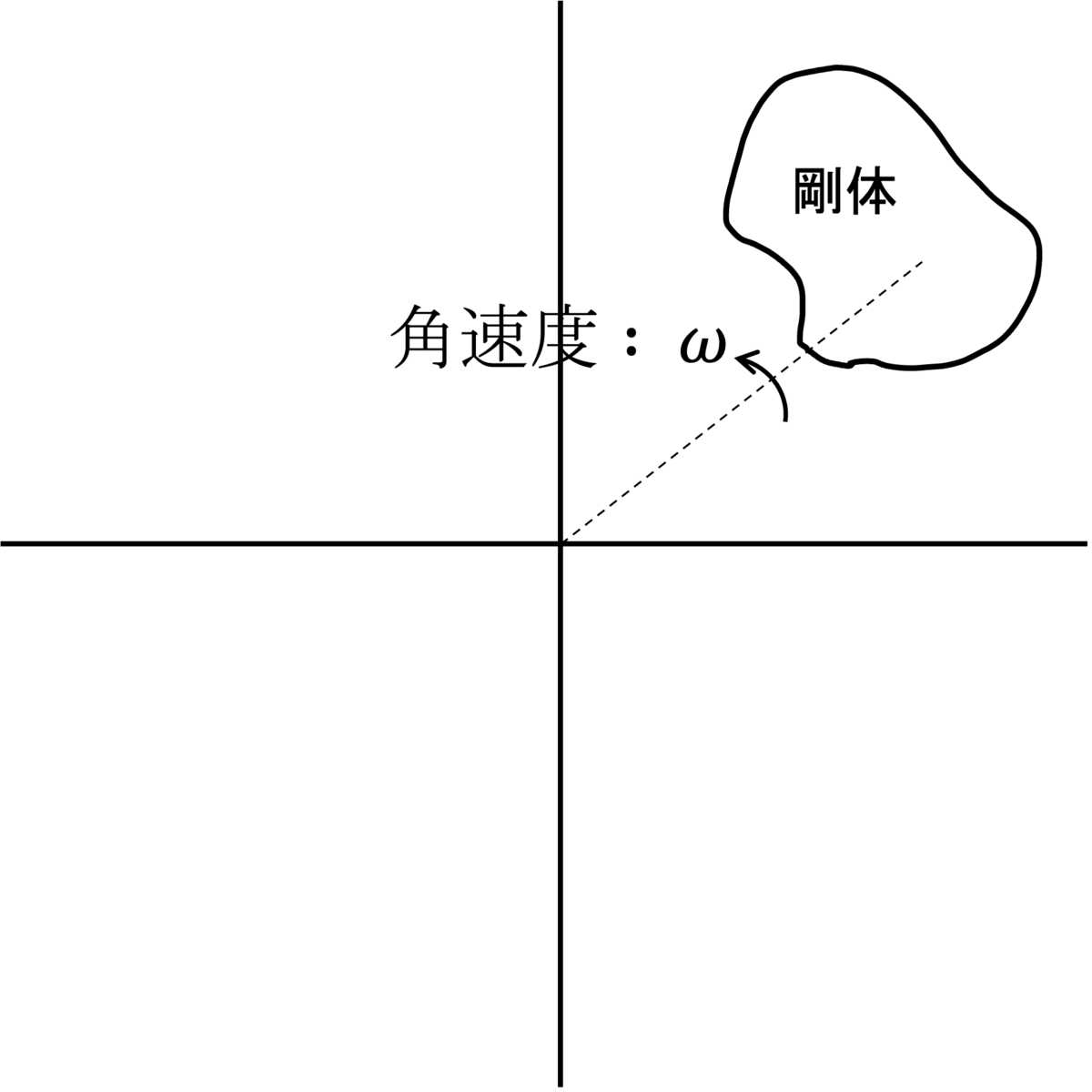
f:id:monologue_physics:20210826142845p:plain

${n}$ 個の質点に分解できたとし、その ${i}$ 番目の質点の質量を ${m_i}$ 、速度を ${\overrightarrow{v_i}}$ 、受ける内力と外力をそれぞれ ${\overrightarrow{f_i} , \, \overrightarrow{F_i} }$ とおく。

剛体全体のみを系として考えるため、内力は構成する別の質点から受ける力、外力はそれ以外から受ける力である。

すると、この質点の運動方程式は

$m_i \frac{d \overrightarrow{v_i}}{dt} = \overrightarrow{f_i} + \overrightarrow{F_i}$

となる。

${n}$ 個の質点全ての運動方程式を足してみる。

作用・反作用の法則によると、ある質点が受ける内力は、それを及ぼした質点に対して同じ大きさで逆向きの反作用を及ぼすから、内力の和は ${\overrightarrow{0}}$ にならなければならない。

よって、運動方程式の和は

$\sum^{n}_{i} m_i \frac{d \overrightarrow{v_i}}{dt} = \sum^{n}_{i} \overrightarrow{F_i}$

となる。

原点周りの回転を考えるのだから、角速度ベクトルをここで導入したい。

角速度ベクトルは、回転が反時計回りに見える方向から観察した時、観察者に向かってくる方向に大きさが角速度となるベクトルである。

つまり、上の図では ${z}$ 軸と同じ方向を向くベクトルとなる。

図を見て考えればわかるだろうが、剛体中のどの質点についても、考える角速度ベクトルは同じであるから、これを質点ごとに別の文字で表す必要はない。

角速度ベクトルを ${\overrightarrow{\omega}}$ とおくと、回転方向の速度は

$\overrightarrow{v_i} = \overrightarrow{\omega} \times \overrightarrow{r_i}$

として外積の計算で表せる。

これを運動方程式に代入すれば

$\sum^{n}_{i} \left( m_i \frac{d \overrightarrow{\omega}}{dt} \times \overrightarrow{r_i} \right) + \sum^{n}_{i} \left( m_i \overrightarrow{\omega} \times \frac{d \overrightarrow{r_i}}{dt} \right) = \sum^{n}_{i} \overrightarrow{F_i}$

となる。

原点を回転の中心としているのだから、 ${\frac{d \overrightarrow{r_i}}{dt} = \overrightarrow{0} }$ である。

よって

${\displaystyle \frac{d \overrightarrow{\omega}}{dt} \times \sum^{n}_{i} m_i \overrightarrow{r_i} = \sum^{n}_{i} \overrightarrow{F_i} }$

となるのだが、左辺の ${ \sum^{n}_{i} m_i \overrightarrow{r_i} }$ というのは重心の位置ベクトルに全体の質量をかけただけのものだから、これでは何も真新しい考察ができない。

そこで、両辺に ${\overrightarrow{r_i}}$ を外積の形で下のようにかけてみる。

$\sum^{n}_{i} \left\{ \overrightarrow{r_i} \times \left( m_i \frac{d \overrightarrow{\omega}}{dt} \times \overrightarrow{r_i} \right) \right\} = \sum^{n}_{i} \overrightarrow{r_i} \times \overrightarrow{F_i}$

左辺の ${\overrightarrow{r_i} \times \overrightarrow{F_i} }$ は力のモーメントと呼ばれ、よく ${\overrightarrow{N}}$ で表される。

てこの原理を考えるときなどに登場する概念である。

方程式を成分ごとに見てみよう。

各成分をあらわに書くと、今回のような回転軸がz軸と一致する時には

$\sum^{n}_{i} m_i \left( -z_ix_i, \, -y_iz_i, \, x_i^2 + y_i^2 \right) \frac{d \omega}{dt} = \sum^{n}_{i} \left( y_iF_{iz} - z_iF_{iy}, \, z_iF_{ix} - x_iF_{iz}, \, x_iF_{iy} - y_iF_{ix} \right)$